Climber Power
Many methods for powering Space Elevator Tether Climbers have been proposed, these include :
Solar Power
Beamed Power (laser, microwave, … )
Transmission along the tether (electricity, vibration)
On-board power storage (chemical, battery/supercapacitor, nuclear, … )
At present the most viable option is considered to be Solar Power, the subject of this page.
the material on this page is based on the presentation and support material prepared by john knapman for the 2013 isec conference
FOR A SOLAR-POWERED CLIMBER…
Power availability and Climber tractive requirement varies along the length of the tether. This paper describes a ‘Constant Speed’ climber concept and the impact on power requirements and tether loading
Solar Power on the Tether
The climb commences at the Earth Port on the Earth’s Equator with only 12 hours of available sunlight each day. The hours of sunlight available to power the climber increases with altitude, but this varies with the time of year.
Earth Axial Tilt = 23.5 degrees
At some times of the year the higher parts of the tether will receive sunlight even when the lowest part is in darkness
trigonometric solution
Basic trigonometry can be used to determine the duration of darkness at different altitudes throughout the year
‘Night’ reduces with altitude
Equinoxes : c. March 21st, September 21st
Solstices : c. June 21st, December 21st
( Day/Night transition is assumed to be when the sun is 50% obscured)
Solar power availability increases with altitude
This graph shows sunlight hours at equinoxes, solstices and dates midway between
(Lines end at GEO)
Climber Power Requirement Changes with Altitude
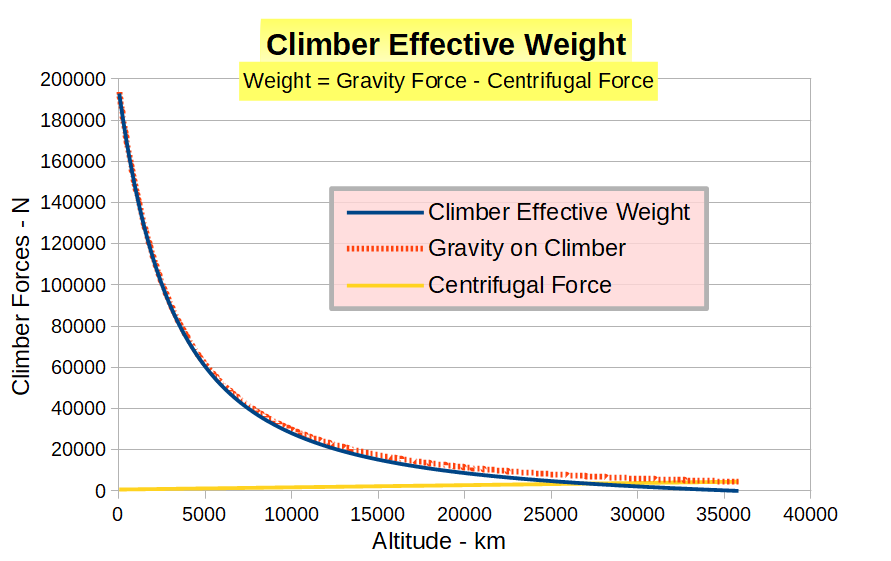
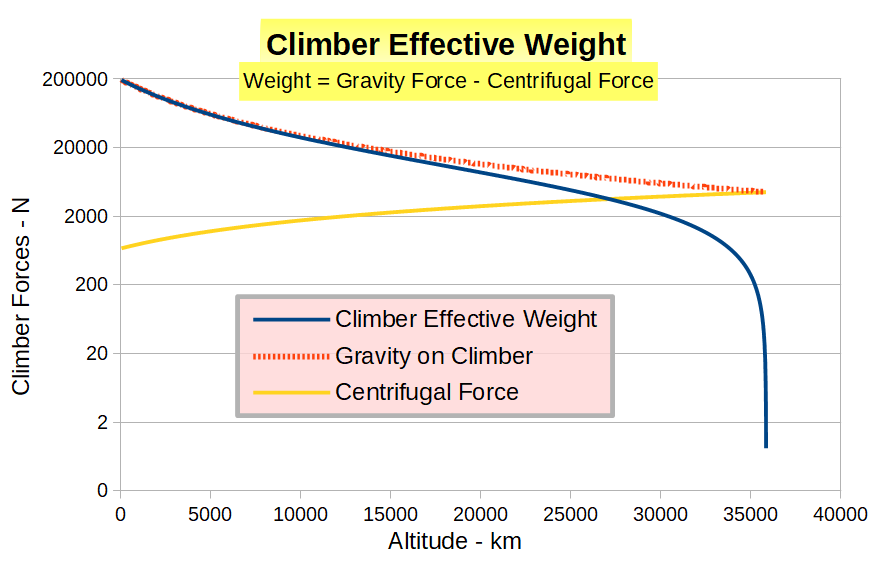
As the climber ascends the tether the effective weight will reduce as the Earth’s gravity force falls and centrifugal force increases. The graphs below show the Gravity and Centrifugal forces on a 20 tonne climber, together with the resultant Effective Weight : one graph uses a conventional linear Y axis, the other uses a logarithmic Y axis to better show the behaviour near GEO.
The tractive power required to drive a climber at any particular speed is directly proportional to the Effective Weight. This means that a climber operating at a constant speed would require maximum power for only a short part of the ascent, with the power supply and traction systems operating at significantly lower levels for the majority of the journey.
This paper proposes another strategy…
maximum Power / maximum Speed Strategy
a more efficient strategy
Significant reduction in climber power and traction system requirements
There are many options for max power and max speed
A more lengthy transit time to GEO means more climbers on the tether (assuming one daily 20-tonne launch). This in turn means a heavier tether will be required.
4 MW power and 300 km/hr max speed yields this speed and power profile
‘Power’ is the tractive power applied to the tether. Drive losses mean that the required electrical power will be higher.
climber distribution
This graphic shows the climber weight distribution, comparing ‘Constant Speed’ and ‘Max Power / Max Speed’ strategies for the same climber transit time of 7 days.
Solar Array sizing for 4 MW power assuming PV efficiency improvements
The required solar array size will be significant but is forecast to have a total mass of 810 kg with speculative technology improvements
The above chart was the status in 2013 : solar cell technology is advancing very fast, with efficiencies of 47.1% achieved in 2019. Mass densities of 10+ kW/kg already appear possible, so a 4MW climber solar cell mass could well be much less than 1 tonne. The 2013 conclusions below are still very valid…
conclusion
The Maximum Power / Maximum Speed strategy has significant benefits. Even higher climber speeds at high altitudes should be considered.